Does Dvr Count Ratings

We ask two questions:
a) Is it important to have an exact placement, either horizontally or vertically, when we take our pictures?
b) If yes, how?
On the first point I will pursue a strategy similar to that followed in mathematical proofs by contradiction. In them. is part of one or more hypotheses, following the relevant arguments and arrive at a contradiction, we will have shown the invalidity of the premises.
What happens if an adequate level of camera?. In fact, in most cases nothing. But there are certain special cases in which the placement is critical. In my personal experience, two situations like this are what I set out below.
One is the making of subjects that occupy much of the frame using a wide angle, usually a building. In this case, if the flatness is not perfect, when we performed the alignment by the editor and activate the subsequent crop, there is a risk that the composition is seriously committed to "cut" any subject area.
The other, perhaps more importantly, is the production of panoramas. Here, if the grading is not adequate, we run two risks. The first is that it is necessary to marry the different takes by hand, since the software may encounter difficulties when trying to do it automatically. Certainly is a cumbersome task. Furthermore, in the final cut we can, as in the previous case, losing the intended composition.
surely more experienced photographers might propose other circumstances in which an appropriate placement is appropriate. Get
leveling is perfect, as is obvious, if we use the camera impossible show of hands, but it is possible using a tripod.
In a previous article on tripods at the end the following sliding Comment:
" One last item I want to say is the presence of a level to achieve perfect flatness. I know that many photographers consider it an important element, but I personally I have not ever found any use ."
This comment reflected the difficulty in obtaining suitable placement if the level was on the tripod. In fact, the only way to achieve this is to stretch or shrink the legs in a trial and error.
time ago, due to the emergence of some slack in the kneecap that initially bought, I bought a new one that incorporates two levels. And the situation varies significantly. Indeed
leveling de un plano se consigue utilizando únicamente dos de los tres grados de libertad que proporciona la rótula. El grado de libertad proporcionado por el giro en un plano horizontal al suelo (o vertical, depende de la posición que adopte la cámara) presupone la horizontalidad ( o verticalidad) de ese plano. Por tanto son los otros dos grados de libertad los que garantizan esta situación. Si disponemos de niveles para ambos, podremos asegurar la adecuada nivelación de nuestras fotografías.

Lineage By Margaret Theme

Equalization in Depth of Field and Focus Distance

Para conocer cómo varía la Profundidad de Campo en función de la Distancia de Enfoque, deberemos basarnos en un par de cosas que ya conocemos, a saber:
a) El tamaño del círculo de confusión depends exclusively on the size of the sensor.
(See the article on the Circle of Confusion).
b) The thin lens equation can be expressed as q = pf / ((p - f).
where:
p is the distance from the objective focal plane.
f is the lens focal length.
q is the distance the image plane, corresponding to the focal plane, the target.
(See article on thin lenses.)
From the knowledge of these facts and taking the example of a normal lens 35 mm for the APS-C, we obtain the value of q for three different focal planes, one located at 100m (100000 mm), one located 10 m (10000 mm) and a third at 1 m (1000 mm) .
q1 = (100000. 35) / (100000 - 35) = 35.01
q2 = (10000. 35) / (10000 - 35) = 35.12
q3 = (1000. 35) / (1000-1935) = 36.27
" do these results mean? Well
focus levels between 100 m and 10 m are their images in a range of
35.12 - 35.01 = 0.11 mm.
and focus levels between 10 m and 1 m are their images in a range of
36.27 - 35.12 = 1.15 mm.
This means that the density of levels is much higher in the first interval in the second. Since, a constant aperture, double inverted cone to a point defined image plane for the circle of confusion is the same, within double inverted cone that are located many more flat image in the first case than in the second and, therefore, the depth of field is greater.
Therefore, we can establish the following rule:
a) If the focus distance increases, the depth of field.
b) If the distance decreases Focus decreasing the depth of field.
This is why the very small depth of field found in the field of photography.

Mtg Sacrificial Bam Deck Ebay

Backlight

Backlight type of photographic situation is fairly well defined. Participates in the following factors:
a) There is a very bright light source in relation to the ambient light (in case it exists). Appears directly in the frame to a greater or lesser extent. Usually occupy a small part of it.
b) Between the lens and light source have a range of subjects. These are illuminated by the source, but have a dark side to the target (strictly, without metaphors).
c) The photographer intention is not to show other details of the dark side of these subjects. Established
these premises, photographic technique for obtaining this kind of photography is very simple. Simply perform a spot metering on the brightest source of light. But like everything in life, there are subtle differences. In fact, depending on the values \u200b\u200bof two independent variables, we get slightly different pictures. One of them is the difference in brightness between the light bulb and the rest. The other is the decision we make about whether to measure exposure at exactly the point of greatest or luminosity or brightness in some slightly lower. In a situation of great contrast of light and measuring the highest point, which appears in the photograph are usually silhouettes.
In the event that the light source is the sun, these photographs are usually done at dawn or dusk. Simply the probability of getting subject line that goes from the lens at the sun is much more likely that when the sun is high in the sky.
With respect to paragraph c) is últil comment that the use of fill flash photography is done in situations that are cousins \u200b\u200bof the backlight, but the photographer's intent here is to balance the brightness of the dark side of the subject (usually a person) the rest of the picture.
The picture that heads this article is an example of a moderate backlight. The dark areas maintain a certain level of detail and do not collapse to pure black. It was taken in the early hours of the morning and can see the sun filtering through the branches of a tree.

Place With Ideas Of Cell Respiration Stories

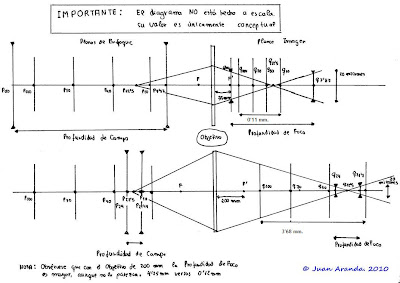
Depth of Field Focal Length

To study the relationship between depth of field depending on the lens focal length, we must rely on a couple of things we already know, namely

a) The size of circle of confusion depends exclusively on the size of the sensor.
(See the article on the Circle of Confusion)
b) The thin lens equation can be expressed as
q = pf / (p - f).
where p is the distance from the objective focal plane.
f is the lens focal length.
q is the distance the image plane, corresponding to the focal plane, the target.
(See: Thin Lenses)
From the knowledge of these facts, calculate the value of q for two different situations concrete ..
In the first, for a 35-mm focal length, get the value of q for two different focal planes, one located 100 m (100000 mm.) And another located 10 m (10000 mm.).
q1 = (100000. 35) / (100000 - 35) = 35.01
q2 = (10000 .35) / (10000 - 35) = 35.12
In the second, for a focal length of 200 mm, we obtain also the value of q for the previous focus planes.
q3 = (100000. 200) / (100000 - 200) = 200.40
q4 = (10000. 200) / (10000 - 200) = 204.08
What these results mean?
Well, for the first case, all planes of focus located between 100 and 10 m levels result image very focused on a range of 35.12 - 35.01 = 0.11 mm.
In the second case, the same planes of focus locate their image planes within a range of 204.08 - 200.40 = 3.68 mm. That is, if the focal length is small (35mm) image planes are much more concentrated than if the focal length is large (200mm).
We can study what happens if we approach a point target at 22.5 m with an aperture of f5.6 and a circle of confusion of 20 microns in diameter (APS-C format).
When using the lens of 35 mm. upper and lower limits of the target area are 7.37me infinity. When we use the target of 200 mm. the same lower and upper limits are now of 21.17 and 24 m. Or what is the same as the area between 10 and 100 m is within the limits of the depth of field when using a 35 mm lens. and much of it is outside when we use the 200mm lens.
The explanation, as can be seen from the figure that appears at the beginning of the article, is that within the limits of the depth of focus that induces the circle of confusion there are many more planes in the first case in the second.
Therefore we can establish the following rule:
a) If the focal length decreases, increasing the depth of field.
b) If the focal length increases they Profunfidad Country.
(It is interesting to note in the same figure that:
If the focal length increases, the depth of focus)