Seductive Essential Oils

Stock: Causes of the blur

In the field of close-up photography, the most important concept to consider is that of Reproduction Ratio, ie "the relationship between the size of the actual subject and its image the sensor. " (See article on photo approach).
In the context of the study on Thin Lenses (See article on Gauss equation ) defined Lateral Increase as "the ratio between the height of the image and the subject's height."
not have to be very insightful to realize that both concepts are equivalent.
this increase was defined lateral m as follows:
and '
m = - ----

and where y 'was the size the image and where and was the size of the subject.
In this article presented the so-called Gauss equation of a thin lens:
January 1 1
---- + ---- = ----
s , s' f
where:
a) s is the distance from subject to optical center of the lens.
b) s' is the distance from the image to the optical center of the lens.
c) f is the focal length of the lens.
In the article on the image plane position and lateral magnification introducing two important observations:
NOTE 1:
When the focal plane is between infinity (∞) and 2 times the focal length, image plane is a distance between 1 and 2 focal lengths.
NOTE 2:
a) If the focal plane is between ∞ and 2 times the focal length is verified that the lateral magnification m is less than unity, which means that the image of the subject is less than the subject itself. This is unusual in photography.
b) If the focal plane is 2 times the focal length is verified that the lateral magnification m is equal to unity.
response to this pair of observations may seem to get pictures of approximation (with reproduction ratios between 1:10 and 1:1) would be feasible for any purpose. To this should be enough to focus at a distance slightly higher than the 2 focal lengths, which would guarantee us getting close to 1 side increases, or what is the same as the size of the image of the subject were somewhat less or equal to the size of one's subject. But it is not .
The reason is simply that the goals can not "focus" very close distances. Depending on cases, between 5 and 15 times the focal length. Or what is the same convergent properties of the targets do not get the rays of light coming out of a point converge into a single image point.
Then: How to achieve breeding ratios in the field of close-up photography?
To understand how this can be done, we must start from the Gauss equation.
1 1 1
As --- + --- = --- if we multiply both sides by s':
, s s'       f

 s'         s'      s'                                      s'      s'
---  +  --- = ----    o, lo que es igual:    --- = ---  - 1
  s         s'      f                                       s       f
In the following figure:

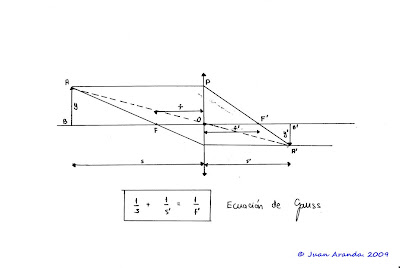
can be seen that in similar triangles ABO and A'B'O verifies that:

A'B 'and' OB 's'
--- = --- = --- = ---
AB , and OB s
; and 's'
Thus m = --- = --- - 1
and f ;

At this point, it should be clear that for increasing m, there are only two possible ways: Either we increase s' or disiminuimos f.
Each of the devices that allow for photos you choose to approach one of these ways:
1) extension rings
These devices are placed between the lens and camera body and their only mission is to remove the sensor from the optical center of the target, thus increasing the value s'. You will find many sites on intenet which displays photographs of various models.
2) Lens approach
This device, similar in appearance to a filter and screw it onto the front of the lens, has a more complex optical properties and will be explained in detail in a later article. It is based on reducing the focal length.